統計学における分散とは？不偏分散との違いも！ 例題でわかりやすく解説

統計学の基礎

統計学・データを理解することにおいて、平均に続いて分散は非常に重要な概念です。

ここでは「分散」という概念について詳しく解説した後、分散から派生した考え方である「不偏分散」についても、意味と定義、求め方をわかりやすく解説していきます。

分散(variance)の意味

統計学において、分散とは数値データのばらつき具合を表すための指標です。ある一つの群の数値データにおいて、平均値と個々のデータの差の２乗の平均を求めることによって計算されます。こうすることによって、平均値から離れた値をとるデータが多ければ多いほど、分散が大きくなります。また、分散を文字式で表す際、 \(s^2\) や \(σ^2\) を使うことが多いです。（\(s^2\)は標本分散。\(σ^2\)は母分散を表すことが多い。）

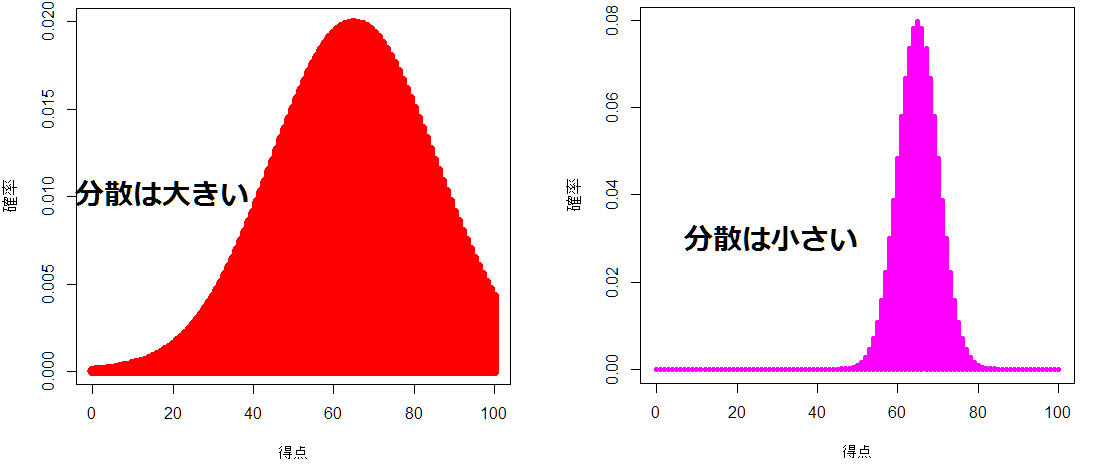
例えば、100点満点のテストにおいて、下図のように平均点から離れた点数の人が多いと分散は大きく、平均点付近に人が集まっている場合分散は小さくなります。

分散の公式

分散の計算は公式の通りにやれば何も難しいことはありません。それは以下の式です。

$$s^2 = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2$$

ここで、文字の説明をすると、nが観測値の数、\(x_1,x_2…x_n\)が一つ一つの観測値。\(x\)の添字は観測したデータの番号を表しています。\(\overline{x}\)はこれらの観測値の平均です。

また、分散は平均との差の二乗の期待値という見方もできるので、確率変数\(X\)の分散\(Var[X]\)は、平均\(μ\)を用いて

$$Var[X] = E[(X-μ)^2] $$

とも表されます。

期待値って何？

計算例

Aさん,Bさん,Cさん,Dさん,Eさんのテストの数学の得点がそれぞれ以下のようになりました。

名前	得点
Aさん	90点
Bさん	80点
Cさん	40点
Dさん	60点
Eさん	90点

この場合、平均点は、

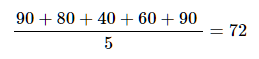
72点となります。さて、分散はどうなるでしょうか？個別の点数と平均点の差の２乗の平均によって求められることから、

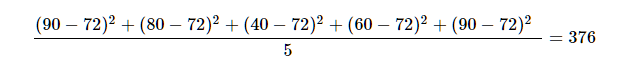
となり、このテストの分散、つまりばらつき具合は376になるということが分かります。

統計学において平均と同様にこの分散も、データを表す大切な指標とされています。

なぜ分散は２乗の和の平均をとるのか？

１つの群における各データの数値の平均からの差、\((\overline{x}-x_1),(\overline{x}-x_2)…(\overline{x}-x_n)\)というのはそれぞれが平均値からどれだけ離れているかを表す指標であり、その値を偏差と呼びます。しかし、これらの値では正と負の両方の値をとってしまいます。それでは、平均値からどれだけ離れているかを表す指標として適切ではありません。２乗することにより、平均値からの距離の基準を正負によらない値として統一することができるのです。

そのため、文字式で表しても\(s^2\) や \(σ^2\)というように２乗を用いて表されます。

また、単に\(s\) や \(σ\)と表されるものは標準偏差と呼ばれ、分散の平方根をとることによって計算される値です。

分散と標準偏差

分散の平方根をとったものを標準偏差といいます。分散は求める過程で、二乗が行われているので、本来の単位とは単位が異なり、そういう意味では少々分かりにくい指標となっています。それを平方根にとることによって単位を揃えたものが標準偏差です。

標準偏差は、例えば模擬試験の偏差値の算出などにも利用されている、身近な指標です。詳しくは→標準偏差の意味と求め方をごらんください。また、偏差値については、偏差値の意味、求め方、性質などのまとめをごらんください。

モーメントを使った分散の求め方

分散は2次モーメント\(E(X^2)\)と、1次モーメント\(E(X)\)を使って求める方法もあります。それが下式です。

$$Var[X] = E(X^2) – [E(X)]^2 = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } x_i^2 -[\frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } x_i]^2$$

この式を言葉でいうと、

$$ 分散 = 二乗の期待値　-　期待値の二乗$$

ということです。この式が成り立つことは、以下のように簡単に証明できます。

証明

\(\begin{eqnarray*}Var[X]  &=& E[(X-μ)^2]\\ &=& E[X^2-2μX+μ^2] \\ &=& E[X^2] -　2μE[X] + μ^2 \\ &=&E[X^2] -　2μ×μ + μ^2\\ &=&E[X^2] – μ^2\\&=&E[X^2] – (E[X])^2 \end{eqnarray*} \)

今回の証明では、期待値の線型性と\(E[X] = μ\)という性質を使いました。→期待値の定義・性質・計算例。平均との違いも！

不偏分散とは？分散との違いは？

分散には、不偏分散（または、標本不偏分散）というややこしい仲間がいます。不偏分散は以下の式で定義されます。

$$S^2 = \frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2 $$

となる\(S^2\)を標本不偏分散（または不偏分散）といいます。これは、母分散の不偏推定量です。これは、標本数を∞に近づけたときに、\(E(S^2) = 母分散\)となる母分散の推定の仕方で、この性質を不偏性と言います。→平均と分散の不偏推定量はどうなるのか？

さて、これは一般的な分散とどのような点において異なるのか？

不偏分散の標本分散との違いは、標本分散は標本のみを考え、その分散であるのに対して、不偏分散は標本の属する母集団全体について考え、その分散の推定値を表しています。母集団と標本の違いは、標本と母集団の違いがすぐわかる説明でまとめているのでそちらも参考にしていただけると幸いです。

統計学の基礎