2016/07/22
2020/05/04
R言語で線形モデルによる回帰分析【第3回】
【第1回】ベクトル・行列の作成と四則演算・要素の参照
【第2回】データ読み込みとデータの取り出し方
【第2.5回】Rで解析する上で知っておきたい便利なコマンド集
【第3回】Rで線形モデルによる回帰分析 ←今ここ!!
【第4回】Rでの自作関数の作り方・使い方
【第5回】グラフのプロットと画像保存の方法(回帰直線)【終】
※R言語入門のトップページはこちら
今回から、いよいよR言語を使って行う解析に入ります。最初の解析は、線形モデルによる回帰分析です。
Rでは様々な解析用・分析用関数が用意されています。そして、次の3種類がR言語で回帰分析用の関数として用意されているものです。
1.lsfit() ……最小二乗法を用いた回帰分析。
2.lm() ……線形モデルを用いた回帰分析。
3.glm() ……一般線形モデルを用いた回帰分析。
今回はこのうちの2つ目。”lm()”という関数を用いて、線形モデルによる回帰分析を行う方法について、説明してきます。Pythonでの回帰分析はこちら→Python3で線形モデルによる回帰分析とプロット
目次
”lm()”関数の使い方
“lm()”関数を用いて、回帰分析を行う場合は以下のように記述します。
もしくは、
lm(y~.,data=dat) #yは目的変数のベクトル。datは解析用に使うデータフレーム
というように記述しても構いません。では、このプログラムは何を示しているのでしょうか。
線形単回帰のモデル式
$$ y = a + bx + ε $$
における,目的変数yと説明変数xをベクトルで指定して、lm関数の引数にします。※¥(ε¥)は誤差項。
つまりR上でのlm関数の使い方は、
もしくは、
ということになるわけです。そうして、Rが回帰係数の予測値を自動で算出してくれます。また、回帰係数\(β=0\)のt検定も自動で行い、p値やt値を簡単に出力できます。
では、この”lm()”関数を実際に使って解析をしてみます。
”lm()”関数を用いて、単回帰分析
では実際に関数”lm()”を使って回帰分析をしてみましょう。そのために、適当な数値を入れたベクトル、x,yを用意します。今回はこのxとyの関係について解析していきます。yを目的変数、xを説明変数に指定します。
x <- c(10,20,10,40,50,10,10,20,70)
これにlm関数を適用させてその結果をansという変数に代入します。
> ans
Call:
lm(formula = y ~ x)Coefficients:
(Intercept) x
0.5965 0.2360
すると、こんな感じになります。この結果から、目的変数yの予測式は、
$$y = 0.5965 + 0.2360x $$
となります。
回帰分析のより詳細な結果を”summary()”関数で抽出
先ほどの結果だと回帰係数しか表示できていませんでしたね。ここで回帰分析の結果に”summary()”という関数を適用させると回帰分析のより詳細なデータをチェックすることができます。summary関数の結果をs.ansという変数に代入して結果を確認してみます。
> s.ans
Call:
lm(formula = y ~ x)Residuals:
Min 1Q Median 3Q Max
-7.3947 -1.9561 -0.0351 1.0439 8.6842Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.59649 2.60529 0.229 0.8254
x 0.23596 0.07739 3.049 0.0186 *
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 4.771 on 7 degrees of freedom
Multiple R-squared: 0.5705, Adjusted R-squared: 0.5091
F-statistic: 9.297 on 1 and 7 DF, p-value: 0.01861
この結果の見方を表にまとめました。
| 項目 | 意味 |
|---|---|
| Estimate | その回帰分析による、回帰係数の推定値(推定値の実現値)。 |
| Multiple R-squared | 決定係数R^2であり、単回帰分析の場合は、xとyの相関係数の2乗がこれを表している。 |
| Pr(>|t|) | p値。回帰係数が0(説明変数は目的変数に影響を与えない)であるという帰無仮説に対する仮設検定結果のp値。 |
| Residual standard error | 誤差項の標準偏差の推定値。 |
| std.Error | 各回帰係数の推定量の標準誤差。 |
| t value | t値。回帰係数=0(説明変数は目的変数に影響を与えない)であるという帰無仮説に対するt検定によって計算される値。 |
解析結果をwrite.tableでcsvファイルに出力
回帰分析した結果をR上で見るだけならいいのですが、出来れば保存しておきたいですよね。後々解析結果を確認したり、ほかの人に見せたりするかもしれません。そんな時にはエクセル(csv)ファイルに結果を出力しましょう。でも、その前に体裁を整える必要があります。これはエクセルファイルに見やすい結果を出力するためです。それが以下のプログラムになります。体裁を整えた結果をresultという変数に代入しています。
coe <- s.ans$coefficient#回帰係数を抽出
aic <- AIC(ans)#AICを抽出
N <- length(y)#解析したデータの総数を抽出
result <- cbind(coe,aic,N) #結果をまとめる
result[2,5:6] <- “” #2行目の5列目と6列目は、上の行と同じなので空にする。
ここでは回帰係数とAICとデータの総数を抽出して変数に格納したあと、resultという変数に全てまとめています。そこで”cbind()”という関数を使っています。この関数は、行数が同じ行列同士を横にしてくっつけて新しい行列を作るというものです。ここではcoe,aic,Nをくっつけています。
これでエクセルファイルに出力するためのデータresultが出来上がりました。エクセルファイルに出力するときには関数”write.table()”というのが用意されているのでそれを使います。
という形で使います。今回はresultという変数を”回帰分析.csv”というファイルに出力します。
オプションとして、
row.names=T ……行名も出力
colnames=F ……列名も出力
を使っています。※T,FはTURE,FALSEでも可。
また、列名とresultの中身を別々に出力しているので、write.tableを2回使用しています。
write.table(result,”回帰分析.csv”,append=T,quote=F,sep=”,”,row.names=T,col.names=F)
これで、今作業しているディレクトリに新しく”回帰分析.csv”というファイルが作成されているはずです。
中身を見るとかこんな感じ。p値,t値、aicなどももきちんと出力されています。

実データを用いた重回帰分析
lmを用いた回帰分析の方法は、ご理解いただけたでしょうか。ここからは、説明変数を複数使う、重回帰分析を実データを用いて紹介していきます。重回帰分析と言っても、使う関数も単回帰分析と変わらず、プログラムの書き方も単回帰分析とほぼ同じです。
↓このデータを使って、解析するので一緒にやる方は是非ダウンロードを!
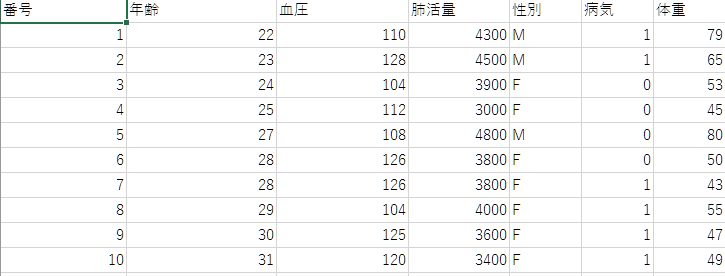
今回は、目的変数に肺活量、説明変数に血圧と体重を入れて重回帰分析をしてみます。まずはデータをデータフレームに読み込みましょう。
df <- read.csv(“sample-data.csv”,header=T,row.names=1)
このdfに回帰分析の関数”lm()”を使います。
※データフレーム$列名 で特定の列を抽出。
以上が重回帰分析のプログラムです。単回帰分析とほとんど変わりありませんよね。違いは説明変数のところに変数が2種類入っていることくらいでしょうか。
重回帰分析をする場合、関数”lm()”は
lm(目的変数のベクトル~説明変数1のベクトル+説明変数2のベクトル+説明変数3ベのクトル)
というような具合で使います。説明変数は複数入れることが可能で、そのときは”+”によって区切るようにして下さい。
結果を整理してエクセルファイルに出力
結果を整理してエクセルファイルに出力するプロセスは、単回帰分析と全く一緒です。標準誤差、t値やp値aic等を出力しましょう。
s.ans <- summary(ans)
coe <- s.ans$coefficient
N <- nrow(df)
aic <- AIC(ans)
result <- cbind(coe,aic,N)
result[2:nrow(result),5:6] <- “”
filename <- “重回帰出力test1.csv”
write.table(matrix(c(“”,colnames(result)),nrow=1),filename,append=T,quote=F,sep=”,”
,row.names=F,col.names=F)
write.table(result,filename,append=T,quote=F,sep=”,”,row.names=T,col.names=F)
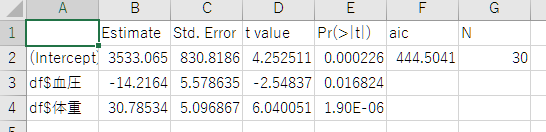
このような結果が出力されました。
重回帰分析プログラムのもう一つの形
lm()関数を用いて重回帰分析する場合、ほかにも書き方があります。その一つがこれから紹介するものです。まずは、変数dfに読み込んだエクセルファイルの中から重回帰分析に使いたい列だけをピックアップします。その結果を新しい変数datに代入します。
dat <- df[,c(3,2,1)]
今回の重回帰分析にはdfの1,2,3列目だけを使用します。そして、目的変数は3列目の肺活量、説明変数に1,2列目の年齢と血圧を使います。
するとこのようなプログラムで重回帰分析できます。
ans <- lm(df$肺活量~.,data=dat)
つまり、
というような具合で使います。目的変数以外の全てが説明変数として利用されます。説明変数が多くなる場合、こちらのほうが完結なプログラムを書けるので便利です。
まとめと復習用コピペプログラム
R言語での回帰分析いかがでしたでしょうか。回帰分析の方法は、分析したいデータをベクトルでまとめて
lm(目的変数~説明変数)
とするだけです。正直、回帰分析の理屈などがあまり分かっていなくても、この第3回の通りにやればRでは回帰分析が出来てしまいます。非常に簡単に出来るのでぜひ覚えておきましょう。ちなみに今回やったようなことをPythonでやりたい方はこちらを参考にしてください。→Python3で線形モデルによる回帰分析とプロット
今回使ったプログラムを全文おいていきますので、復習用に使ってください。
#とりあえず単回帰分析
y <- c(1,3,4,10,5,1,3,14,21)
x <- c(10,20,10,40,50,10,10,20,70)
ans <- lm(y~x)#回帰分析を実行
ans
s.ans <- summary(ans)#回帰分析の詳細結果抽出
s.ans
coe <- s.ans$coefficient#回帰係数を抽出
#coe <- coef(s.ans)やs.ans$coefも同じ出力
N <- length(y)
aic <- AIC(ans)
result <- cbind(coe,aic,N)
result[2,5:6] <- ""
result
#結果をcsvファイルへ出力
write.table(matrix(c("",colnames(result)),nrow=1),"回帰分析.csv",append=T,quote=F,sep=",",row.names=F,col.names=F)
write.table(result,"回帰分析.csv",append=T,quote=F,sep=",",row.names=T,col.names=F)
#csvファイルを用いた重回帰分析
df <- read.csv("sample-data.csv",header=T,row.names=1,fileEncoding="CP932")
###重回帰分析###
#列名で指定
ans <- lm(df$肺活量~df$血圧+df$体重)
s.ans <- summary(ans)
coe <- s.ans$coefficient
N <- nrow(df)
aic <- AIC(ans)
result <- cbind(coe,aic,N)
result[2:nrow(result),5:6] <- ""
write.table(matrix(c("",colnames(result)),nrow=1),filename,append=T,quote=F,sep=","
,row.names=F,col.names=F)
filename = "重回帰出力test1"
write.table(result,filename,append=T,quote=F,sep=",",row.names=T,col.names=F)
write.table("",filename,append=T,quote=F,sep=",",row.names=F,col.names=F)
#列番号で指定
dat <- df[,c(3,2,1)]
ans <- lm(df$肺活量~.,data=dat)
s.ans <- summary(ans)
coe <- s.ans$coefficient
N <- nrow(df)
aic <- AIC(ans)
result <- cbind(coe,aic,N)
result[2:nrow(result),5:6] <- ""#excelに複数のデータの結果を付け加えるときにはappendをTにする
filename <- "重回帰出力test2.csv"
write.table(matrix(c("",colnames(result)),nrow=1),filename,append=T,quote=F,sep=","
,row.names=F,col.names=F)
write.table(result,filename,append=T,quote=F,sep=",",row.names=T,col.names=F)
【第1回】ベクトル・行列の作成と四則演算・要素の参照
【第2回】データ読み込みとデータの取り出し方
【第2.5回】Rで解析する上で知っておきたい便利なコマンド集
【第3回】Rで線形モデルによる回帰分析 ←今ここ!!
【第4回】Rでの自作関数の作り方・使い方
【第5回】グラフのプロットと画像保存の方法(回帰直線)【終】
※R言語入門のトップページはこちら








Recommended