2016/07/22
2020/05/04
Rでロジスティック回帰分析 そのまま使える自作関数例
今回はRによるロジスティック回帰分析の方法をご紹介します。また、「ロジスティック回帰分析をして、必要なデータを抽出しファイルに書き出す」までの一連の流れを自作関数にまとめたので、解析をお急ぎの方はそちらも参考にして頂ければ幸いです。
※ここではロジスティック回帰について解説しています。線形モデルによる回帰分析は、入門コーナーの記事であるR言語で線形モデルによる回帰分析でまとめているのでそちらをごらんください。
※R言語について、さらに学びたい方はR言語入門をご覧ください。
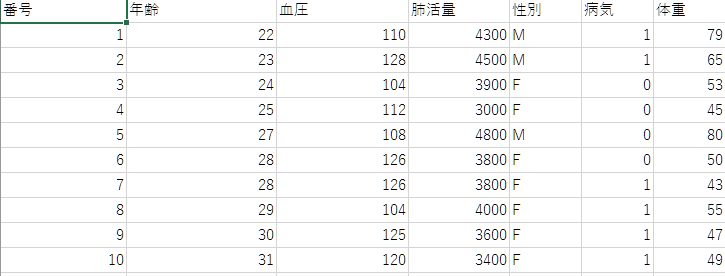
今回、説明用に用いるデータです。↓
目次
ロジスティック回帰分析とは
そもそもロジスティック回帰分析とはどのような、解析手法なのでしょうか。解析に入る前に、簡単に触れておきますね。
どのようなときに使われるのか?ズバリ、目的変数のデータが2値であらわされているときです。
例えば、下の写真のようなデータを、解析したいとします。病気を目的変数、体重と肺活量は説明変数に設定します。

このとき、一般的な線形回帰分析を行うときは、
$$y = β_0 + β_1x_1 + β_2x_2$$
というようなモデル式において、最小二乗法を用いて、できるだけ正確にyを推定できるように係数を定めていました。しかし、今回の目的変数である病気というのは、0か1の値しかとりません。
このようなデータを統計分析する場合、通常の回帰分析よりも、ロジスティック回帰分析を行うのが好ましいです。ロジスティック回帰モデルでは、結果が1となる確率をpとおいて次のようなモデル式で推定します。
$$log(\frac{ p }{ 1-p }) = β_0 + β_1x_1 + β_2x_2$$
この式を最尤法を用いてできるだけ正確に成り立つように回帰係数を推定します。また、この関数はロジット関数と呼ばれることがあります。\(logit(p)\)や\(logit(π)\)などと書かれたものを見かけたら、このロジット関数の意味です。
ここで目的変数はpという確率で1になり、1-pという確率で0になる2項分布について考えることになります。一般的な線形回帰モデルが直線になるのに対して、ロジスティック回帰では対数オッズによる曲線となるのが特徴です。
“glm()”によるロジスティック回帰分析
それでは、実際にRでロジスティック回帰分析を行っていきましょう!もし、理論が完全に分からなくても、Rでは簡単に分析が出来てしまいます。というのは、普通の回帰分析と大した違いはなく、”lm()”の代わりに関数glm()を用いるだけです。このglmの使い方を見ていきましょう。
データの読み込み
まずは変数dfにデータを、データフレームとして読み込みます。このデータは1行目が列名になっていることと、1列目が行番号になっていることに注意して、header=Tとrow.names=1を指定します。
解析に使うデータのみを抽出
ロジスティック回帰モデルでは説明変数がお互いに独立な変数であることが望ましいですが、今回は独立であるかを説明するのがメインではないので、それは考えずに、
目的変数:病気
説明変数:年齢、血圧、体重
として解析を行います。
ロジスティック回帰分析に使うデータはdfの5,1,2,6列目になるので、以下のようなプログラムで解析に使う部分だけを抽出して変数datに代入します。
glm()でロジスティック回帰分析する方法
先でも述べましたが、ロジスティック回帰分析は、一般線形モデルを用いた回帰分析用の”glm()”という関数が用意されているのでこれを使います。
このとき、以下のように記述します。
ここで、ロジスティック回帰分析の回帰モデルに従って、引数である《family》に《family=binomial》が指定されていることに注意しましょう。これによって、二項分布の指定を行っています。(二項分布ついては二項分布のわかりやすいまとめをご覧ください。)
よって、以下のようなプログラムになります。
結果の見方と取り出し方
まずは”summary()”によって解析結果ansの詳細を確認しましょう。ここでは詳細をs.ansという変数に代入します。
> s.ans
Call:
glm(formula = df$病気 ~ ., family = binomial, data = dat)Deviance Residuals:
Min 1Q Median 3Q Max
-2.0729 -1.0128 0.5562 0.8537 1.4564Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.27037 5.62695 -1.114 0.2651
年齢 0.00172 0.04477 0.038 0.9694
血圧 0.01697 0.04457 0.381 0.7033
体重 0.08019 0.03878 2.068 0.0387 *
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 40.381 on 29 degrees of freedom
Residual deviance: 34.698 on 26 degrees of freedom
AIC: 42.698Number of Fisher Scoring iterations: 4
このようになっているはずです。線形回帰分析による、各種予測値が表示されています。この中から欲しいデータを抽出していきます。
$coefficientで回帰係数、標準誤差、z値、p値を抽出
これらをs.ans$coefficientにより抽出します。
> coe
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.270371644 5.62695444 -1.11434555 0.26513097
年齢 0.001719847 0.04476968 0.03841544 0.96935645
血圧 0.016973168 0.04456912 0.38082798 0.70333090
体重 0.080190137 0.03878173 2.06772960 0.03866546
s.ans$coefficientとすると、行列のような形で結果が抽出されます。
左から、回帰係数・標準誤差(SE)・z値・p値です。
オッズ比とオッズ比の95%信頼区間を出力
これらはロジスティック回帰分析の場合expを用いて以下のように抽出できます。
RRlow <- exp(coe[,1]-1.96*coe[,2])
RRup <- exp(coe[,1]+1.96*coe[,2])
AICと要素数を抽出
解析に使った要素(ベクトル)の長さとAICも抽出しておきましょう。
“nrow()”と”AIC()”を用いて以下のプログラムで出来ます。
aic <- AIC(ans)
結果を変数resultにまとめてcsvファイルに書き出し
後から確認できるように、解析結果をresultという変数にまとめてエクセルファイル(csv形式)に書き出します。
今回は、オッズ比の95%信頼区間の部分は列名が入っていないので、列名を入れるために以下のプログラムを一行追加しました。
colnames(result)[6:7] <- c(“RR95%CI.low”,”RR95%CI.up”)
また、違う行に同じ値が入ってしまっているところがあるので、そこは以下のプログラムで空欄を入れることによって消してあげましょう。
最後に書き出して終了です。
write.table(result,file,append=T,quote=F,sep=”,”,row.names=T,col.names=F)
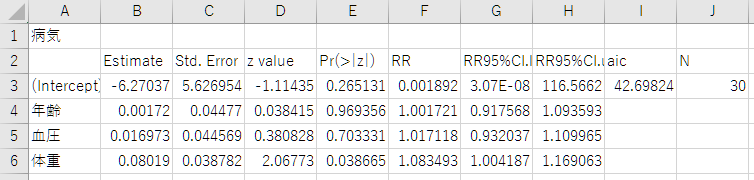
エクセルで確認すると以下のような結果になりました。

最初の列には説明変数が入っています。目的変数(応答変数)はここでは書かれていませんが”病気”です。この解析の場合、体重のp値だけ0.05より小さくなっているので、有意水準0.05だとすれば、体重のみ有意な説明変数となります。
そのまま使えるロジスティック回帰分析の自作関数
ロジスティック回帰分析のプログラムは長いですよね。解析量が多いとき、毎回この長いプログラムを書くのは大変です。そこで、一連の流れをまとめた自作関数を作って、解析するときはその関数を呼び出すことによって、毎回プログラムを書く手間を省きます。
今回の関数は、
までの一連の流れを組み込んであります。これによって、プログラムが大分すっきりします。
自作関数”logi_fun()”
引数には、
解析用データ、出力ファイルの名前、目的変数の名前
を取るように作ってあります。
logi_fun <- function(data,file,disease){
ans <- glm(data$Y~.,data=data,family=binomial)
s.ans <- summary(ans)
coe <- s.ans$coefficient
RR <- exp(coe[,1])
RRlow <- exp(coe[,1]-1.96*coe[,2])
RRup <- exp(coe[,1]+1.96*coe[,2])
N <- nrow(data)
aic <- AIC(ans)
result <- cbind(coe,RR,RRlow,RRup,aic,N)
colnames(result)[6:7] <- c(“RR95%CI.low”,”RR95%CI.up”)
if(nrow(result)>=2){
result[2:nrow(result),8:9] <- “”
}
write.table(disease,file,append=T,quote=F,sep=”,”,row.names=F,col.names=F)
write.table(matrix(c(“”,colnames(result)),nrow=1),file,append=T,quote=F,sep=”,”,row.names=F,col.names=F)
write.table(result,file,append=T,quote=F,sep=”,”,row.names=T,col.names=F)
write.table(“”,file,append=T,quote=F,sep=”,”,row.names=F,col.names=F)
}
“logi_fun()”を使ってロジスティック回帰分析をしてみる
先ほどの関数を丸々Rに読み込ませて、logi_funが使えるようにしておきましょう。
解析用のデータを作る
目的変数:病気
説明変数:年齢、血圧、体重
によるロジスティック重回帰分析をしてみましょう。まずは、解析用のデータ作ります。
データをデータフレーム型で読み込んで、
解析に使う列だけを取り出し、datという変数に格納します。
目的変数の列名を”Y”に変更
今回の関数は目的変数の列名を”Y”で指定しています。
この部分です。これは、この関数がどのようなデータ、どのような名前の目的変数にも対応出来るように”Y”という名前の列を目的変数に取るように設定しています。つまり、解析するデータの目的変数の列名を”Y”に変更してから関数を適用させる必要があるのです。
そのために、今回はdatの1列目を目的変数をしたいので、1列目の列名を”Y”にします。
これで準備は整いました。
プログラムの実行
今回は目的変数が病気であるということ、書き出すファイルの名前を”logistic_sample.csv”とすることにして関数を使います。
これで、解析が完了しました。このような結果になります。全く同じ結果になりましたね。
今回使ったコマンドや関数
いかがでしたでしょうか。ロジスティック回帰分析といえど、R上でプログラミングによって解析する上では重回帰分析と大して変わらないということがお分かりいただけたと思います。目的変数が今回のような2値データの解析を行うときは是非使ってみてください。今回使った関数やコマンドを一覧でまとめておきました。
| プログラム | 使い方 |
|---|---|
| glm() | 一般線形モデルを用いた回帰分析。glm(目的変数のベクトル~.,解析データ)で、解析を実行。ロジスティック回帰の場合は《family=binomial》を指定。 |
| summary() | 回帰分析の要約が表示される。回帰分析の結果を引数にすることで、より詳細な結果を表示する。 |
| $coefficient | 今回のロジスティック回帰分析の場合、summary()によって詳細を抽出した回帰分析の結果に対して、回帰係数,標準誤差,z値,p値を抽出する。 |
| AIC | 回帰分析のAICを抽出。 |
| logi_fun() | 当サイトによる自作関数。引数に解析データ、出力ファイル名、目的変数名を取る。ロジスティック回帰分析を行い、回帰係数、標準誤差、z値、p値、RR、95%信頼区間、AIC、データの要素数をcsvファイルに出力。 |
R言語について、さらに学びたい方はR言語入門をご覧ください。








Recommended